背包问题总结

 Algorithm
 

0/1背包问题

  • 描述：

有$N$件物品和一个容量是$V$的背包。

第$i$件物品的体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 1000$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行两个整数$v_i$和$w_i$，$0 < v_i,w_i \le 1000$，用空格隔开，分别表示第$i$件物品的体积和价值。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2
2 4
3 4
4 5

  • 样例输出：

8

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
using namespace std;

const int N=1010;
int n,m;
int f[N];

int main() {
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int c,w;
        cin>>c>>w;
        for(int j=m;j>=c;j--)
            f[j]=max(f[j],f[j-c]+w);
    }
    cout<<f[m]<<endl;
    return 0;
}

完全背包问题

  • 描述：

有$N$种物品和一个容量是$V$的背包，每种物品都有无限件可用。

第$i$种物品的体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 1000$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行两个整数$v_i$和$w_i$，$0 < v_i,w_i \le 1000$，用空格隔开，分别表示第$i$种物品的体积和价值。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2
2 4
3 4
4 5

  • 样例输出：

10

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int f[N];

int main() {
    cin>n>>m;
    for(int i=0;i<n;i++) {
        int c,w;
        cin>>c>>w;
        for(int j=c;j<=m;j++)
            f[j]=max(f[j],f[j-c]+w);
    }
    int res=0;
    for(int i=0;i<=m;i++) res=max(res,f[i]);
    cout<<res<<endl;
    return 0;
}

多重背包问题

  • 描述：

有$N$种物品和一个容量是$V$的背包。

第$i$种物品最多有$s_i$件，每件体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且价值总和最大。
输出最大价值。

暴力 O(N*M*S)
  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 100$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行三个整数$v_i$、$w_i$和$s_i$，$0 < v_i,w_i,s_i \le 100$，用空格隔开，分别表示第$i$件物品的体积、价值和数量。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2 3
2 4 1
3 4 3
4 5 2

  • 样例输出：

10

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
using namespace std;

const int N=110;

int n,m;
int f[N];

int main() {
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int c,w,s;
        cin>>c>>w>>s;
        for(int j=m;j>=0;j--)
            for(int k=1;k<=s;k++)
                if(j>=k*c)
                    f[j]=max(f[j],f[j-k*c]+k*w);
    }
    cout<<f[m]<<endl;
    return 0;
}
二进制优化 O(N*M*log S)
  • 输入：

第一行两个整数$N$和$V$，$0 < N \le 1000$，$0 < V \le 2000$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行三个整数$v_i$、$w_i$和$s_i$，$0 < v_i,w_i,s_i \le 2000$，用空格隔开，分别表示第$i$件物品的体积、价值和数量。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2 3
2 4 1
3 4 3
4 5 2

  • 样例输出：

10

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

const int N=2010;

int n,m;
int f[N];
struct Good {
    int v,w;
};
int main() {
    vector<Good> goods;
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int v,w,s;
        cin>>v>>w>>s;
        for(int k=1;j<=s;k*=2) {
            s-=k;
            goods.push_back({v*k,w*k});
        }
        if(s>0) goods.push_back({v*s,w*s});
    }
    for(auto good:goods)
        for(int j=m;j>=good.v;j--)
            f[j]=max(f[j],f[j-good.v]+good.w);
    cout<<f[m]<<endl;
    return 0;
}
单调队列优化 O(N*M)
  • 输入：

第一行两个整数$N$和$V$，$0 < N \le 1000$，$0 < V \le 20000$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行三个整数$v_i$、$w_i$和$s_i$，$0 < v_i,w_i,s_i \le 20000$，用空格隔开，分别表示第$i$件物品的体积、价值和数量。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2 3
2 4 1
3 4 3
4 5 2

  • 样例输出：

10

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;

const int N=20010;

int n,m;
int f[N],g[N],q[N];

int main() {
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int c,w,s;
        cin>>c>>w>>s;
        memcpy(g,f,sizeof f);

        for(int j=0;j<c;j++) {
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=c) {
                f[k]=g[k];
                if(hh<=tt&&k-s*c>q[hh]) hh++;
                if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/c*w);
                while(hh<=tt&&g[q[tt]]-(q[tt]-j)/c*w<=g[k]-(k-j)/c*w) tt--;
                q[++tt]=k;
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

混合背包问题

  • 描述：

有$N$种物品和一个容量是$V$的背包。

物品一共有三类：

  • 第一类物品只能用1次（01背包）
  • 第二类物品可以用无限次（完全背包）
  • 第三类物品最多只能用$s_i$次（多重背包）

每种体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且价值总和最大。
输出最大价值。

  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 1000$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行三个整数$v_i$、$w_i$和$s_i$，用空格隔开，分别表示第$i$件物品的体积、价值和数量。

$0 < v_i,w_i \le 1000$，$-1 \le s_i \le 1000$。

  • $s_i=-1$表示第$i$种物品只能用1次
  • $s_i=0$表示第$i$种物品可以用无限次
  • $s_i>0$表示第$i$种物品可以使用$s_i$次
  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5
1 2 -1
2 4 1
3 4 0
4 5 2

  • 样例输出：

8

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N=1010;

int n,m;
int f[N];

struct Thing {
    int kind;
    int v,w;
};
vector<Thing> things;

int main() {
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int v,w,s;
        cin>>v>>w>>s;
        if(s<0) things.push_back({-1,v,w});
        else if(s==0) things.push_back({0,v,w});
        else {
            for(int k=1;k<=s;k*=2) {
                s-=k;
                things.push_back({-1,v*k,w*k});
            }
            if(s>0)things.push_back({-1,v*s,w*s});
        }
    }
    for(auto thing : things) {
        if(thing.kind<0) {
            for(int j=m;j>=thing.v;j--) f[j]=max(f[j],f[j-thing.v]+thing.w);
        }else {
            for(int j=thing.v;j<=m;j++) f[j]=max(f[j],f[j-thing.v]+thing.w);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

二维费用的背包问题

  • 描述：

有$N$件物品和一个容量是$V$的背包，背包能承受的最大重量是$M$。

每件物品只能用一次。体积是$v_i$，重量是$m_i$，价值是$w_i$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

  • 输入：

第一行三个整数$N$、$V$和$M$，$0 < N \le 1000$，$0 < V,M \le 100$，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有$N$行，每行三个整数$v_i$、$m_i$和$w_i$，$0 < v_i,m_i \le 100$，$0 < w_i \le 1000$，用空格隔开，分别表示第$i$件物品的体积、重量和价值。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

  • 样例输出：

8

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<algorithm>
using namespace std;

const int N=110;

int n,v,m;
int f[N][N];

int main() {
    cin>>n>>v>>m;
    for(int i=0;i<n;i++) {
        int a,b,c;
        cin>>a>>b>>c;
        for(int j=v;j>=a;j--)
            for(int k=m;k>=b;k--)
                f[j][k]=max(f[j][k],f[j-a][k-b]+c);
    }
    cout<<f[v][m]<<endl;
    return 0;
}

分组背包问题

  • 描述：

有$N$组物品和一个容量是$V$的背包。

每组物品有若干个，同一组内的物品最多只能选一个。

每件物品的体积是$v_{ij}$，价值是$w_{ij}$，其中$i$是组号，$j$是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

  • 输入：

第一行有两个整数$N$和$V$，$0 < N,V \le 100$，用空格隔开，分别表示物品组数和背包容量。

接下来有$N$组数据：

  • 每组数据第一行有一个整数$S_i$，$0 < S_i \le 100$，表示第$i$个物品组的物品数量；
  • 每组数据接下来有$S_i$行，每行有两个整数$v_{ij}$和$w_{ij}$，$0 < v_{ij},w_{ij} \le 100$，用空格隔开，分别表示第$i$个物品组的第$j$个物品的体积和价值。
  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

3 5
2
1 2
2 4
1
3 4
1
4 5

  • 样例输出：

8

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=110;

int n,m;
int f[N],v[N],w[N];

int main() {
    cin>>n>>m;
    for(int i=0;i<n;i++) {
        int s;
        cin>>s;
        for(int j=0;j<s;j++) cin>>v[j]<<w[j];
        for(int j=m;j>=0;j--)
            for(int k=0;k<s;k++)
                if(j>=v[k])
                    f[j]=max(f[j],f[j-v[k]]+w[k]);
    }
    cout<<f[m]<<endl;
    return 0;
}

背包问题求方案数

  • 描述：

有$N$件物品和一个容量是$V$的背包，每件物品只能使用一次。

第$i$件物品的体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最优选法的方案数，注意答案可能很大，请输出答案模$10^9+7$的结果。

  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 1000$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行两个整数$v_i$和$w_i$，$0 < v_i,w_i \le 1000$，用空格隔开，分别表示第$i$件物品的体积和价值。

  • 输出：

输出一个整数，表示方案数模$10^9+7$的结果。

  • 样例输入：

4 5
1 2
2 4
3 4
4 6

  • 样例输出：

2

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N=1010,mod=1000000009,INF=1000000;
int n,m;
int f[N],g[N];

int main() {
    cin>>n>>m;
    g[0]=1;
    for(int i=1;i<=m;i++) f[i]=-INF;
    for(int i=0;i<n;i++) {
        int v,w;
        cin>>v>>w;
        for(int j=m;j>=v;j--) {
            int t=max(f[j],f[j-v]+w);
            int s=0;
            if(t==f[j])s+=g[j];
            if(t==f[j-v]+w)s+=g[j-v];
            if(s>=mod)s-=mod;
            f[j]=t;
            g[j]=s;
        }
    }
    int maxw=0;
    for(int i=0;i<=m;i++) maxw=max(maxw,f[i]);
    int res=0;
    for(int i=0;i<=m;i++)
        if(maxw==f[i]) {
            res+=g[i];
            if(res>=mod) res-=mod;
        }
    cout<<res<<endl;
    return 0;
}

求背包问题的方案

  • 描述：

有$N$件物品和一个容量是$V$的背包，每件物品只能使用一次。

第$i$件物品的体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是$1…N$。

  • 输入：

第一行两个整数$N$和$V$，$0 < N,V \le 1000$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行两个整数$v_i$和$w_i$，$0 < v_i,w_i \le 1000$，用空格隔开，分别表示第$i$件物品的体积和价值。

  • 输出：

输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。

物品编号范围是$1…N$。

  • 样例输入：

4 5
1 2
2 4
3 4
4 6

  • 样例输出：

1 4

  • 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

const int N=1010;

int n,m;
int v[N],w[N],f[N][N];

int main() {
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=n;i>=1;i--) {
        for(int j=0;j<=m;j++) {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    int vol=m;
    for(int i=1;i<=n;i++) {
        if(f[i][vol]==f[i+1][vol-v[i]]+w[i]) {
            cout<<i<<' ';
            vol-=v[i];
        }
    }
    return 0;
}

有依赖的背包问题

非树形依赖的背包问题
  • 描述：

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过$N$元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

|主件| 附件|

|电脑| 打印机，扫描仪|

|书柜| 图书|

|书桌| 台灯，文具|

|工作椅| 无|

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的$N$元。于是，他把每件物品规定了一个重要度，分为5等：用整数1−5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是10元的整数倍）。他希望在不超过$N$元（可以等于$N$元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第$j$件物品的价格为$v_[j]$，重要度为$w_[j]$，共选中了$k$件物品，编号依次为$j_1,j_2,…,j_k$，则所求的总和为：
$$v_[j_1] \times w_[j_1]+v_[j_2] \times w_[j_2]+ …+v_[j_k] \times w_[j_k]$$

请你帮助金明设计一个满足要求的购物单。

  • 输入：

第1行为两个正整数$n$和$m$，分别表示总钱数和希望购买物品的个数，$n<32000$，$m<60$，用空格隔开。

从第2行到第$m+1$行，第$j$行给出了编号为$j-1$的物品的基本数据，每行有3个非负整数$v$、$p$、$q$，分别表示该物品的价格、重要度（1-5）、是主件还是附件，$q=0$表示该物品为主件，$q>0$表示该物品为附件且$q$是所属主件的编号，$v<10000$。

  • 输出：

一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值。

  • 样例输入：

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

  • 样例输出：

2200

  • 解题思路：分组背包

  • 参考代码：

    1
    2


树形依赖的背包问题
  • 描述：

有$N$个物品和一个容量是$V$的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

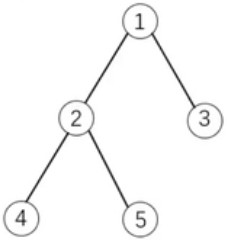
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是$i$，体积是$v_i$，价值是$w_i$，依赖的父节点编号是$p_i$，物品的下标范围是$1…N$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

  • 输入：

第一行两个整数$N$和$V$，$1 \le N,V \le 100$，用空格隔开，分别表示物品个数和背包容量。

接下来有$N$行数据，每行数据表示一个物品。
第$i$行有三个整数$v_i$,$w_i$,$p_i$，$1 < v_i,w_i \le 100$，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
$p_i==-1$表示根节点，$1 \le p_i \le N$表示内部节点，数据保证所有物品构成一棵树。

  • 输出：

输出一个整数，表示最大价值。

  • 样例输入：

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

  • 样例输出：

11

  • 解题思路：分组背包+树形dp

  • 参考代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n,m;
int h[N],e[N],ne[N],idx;
int v[N],w[N],f[N][N];
void add(int a,int b) {
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u) {
    for(int i=h[u];i!=-1;i=ne[i]) {
        int son=e[i];
        dfs(son);
        for(int j=m-v[u];j>=0;j--)
            for(int k=0;k<=j;k++)
                f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
    }
    for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];
    for(int i=0;i<v[u];i++) f[u][i]=0;
}
int main() {
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int root;
    for(int i=1;i<=n;i++) {
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1) root=i;
        else add(p,i);
    }
    dfs(root);
    cout<<f[root][m]<<endl;

    return 0;
}
 Previous

String