两道算法编程题

 Algorithm
 

数组排序

  • 描述：

你需要对一个数组进行排序（升序），每一次，你可以将一个数移动到任意位置，这一次操作的代价是这个数的大小。最少需要多少代价才能将整个数组排序？

  • 输入：

第一行输入一个正整数N，$1 \le N \le 100$，表示数组元素个数。

第二行输入N个整数，整数之间用空格隔开。

  • 输出：

输出一个整数，表示将整个数组排序的最小代价。

  • 样例输入：

4
8 1 2 3

  • 样例输出：

6

  • 解题思路：

求出里面和最大的升序数组，用数组和减去它就是结果了。因为最终的数组和原来的数组，差别就在于那些移动了位置的数，要让移动位置的代价最小，当然就是让移动位置的数的和最小，等价于不移动位置的数的和最大，而最大的升序数组和就是能够不移动位置的最大子数组。
最大的升序数组和可用dp求出。

  • 参考代码:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #include<iostream>
    #include<algorithm>

    using namespace std;


    int main() {
        
        return 0;
    }

取棋子

  • 描述：

西西有一个N行N列的棋盘，其中某些格子上放有棋子（黑子或白子）。西西不希望棋盘上有两个相邻的格子放 着颜色相同的棋子，与第i行 第j列的格子相邻的格子为：

第i-1行第j列的格子（当i>1时）；

第i+1行第j列的格子（当i<N时）；

第i行第i-1列的格子（当i>1时）；

第i行第i+1列的格子（当i<N时）。

现在，西西可以取走棋盘上的某些棋子，使得剩下的棋子中，任意两个颜色相同的棋子所在的格子不相邻。
那么， 棋盘上最多剩下多少个棋子？

  • 输入：

第一行输入一个正整数N，$N \le 50$，表示棋盘的行列数。

接下来的N行，每行有N个整数，整数之间用空格隔开，表示棋盘每行每列防止棋子的情况。
整数取值只能是0、1、2，分别表示该格未放棋子、放的是黑子、放的是白子。

  • 输出：

输出一个整数，表示棋盘上最多剩下的棋子数。

  • 样例输入：
  • 样例输出：
  • 解题思路：

给每个棋子设置一个度(0 1 2 3 4)。一个棋子周围每有一个同样颜色的棋子，那就让它的度加1，最小为0，最大为4。然后从棋盘里逐个删掉度是4的并且更新棋盘(周围的同样颜色的棋子度要剪1)，然后删掉度是3的，以此类推知道所有棋子度是0，看这时候删了多少棋子。

用4个hash set分别保存度为1 2 3 4的点，每删一个度为4的点，就更新所有它周围的节点，然后再继续进行删除。对黑的进行一次删除，再对白的进行一次删除，就能求出结果了。

这个方法对相连的度为4的点还要额外讨论。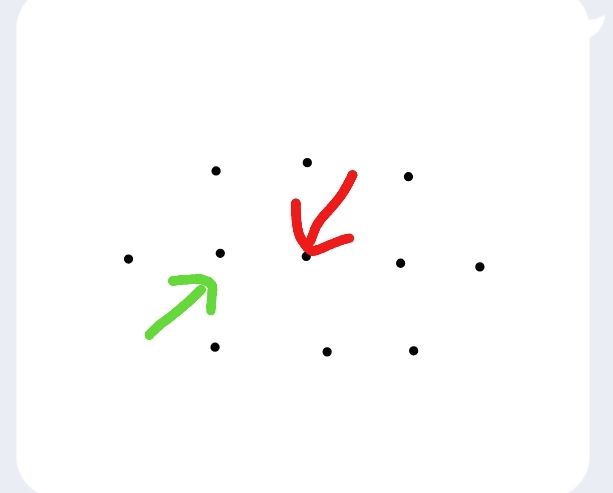

图中的两个点度都为4，但删绿的总共删四个，删红的 总共删五个。
所以又想出一个方法：先取连通的区域 统计如果在国际象棋棋盘中 黑格和白格点数 然后删少的。
在上图中就是黑7白4，删白的。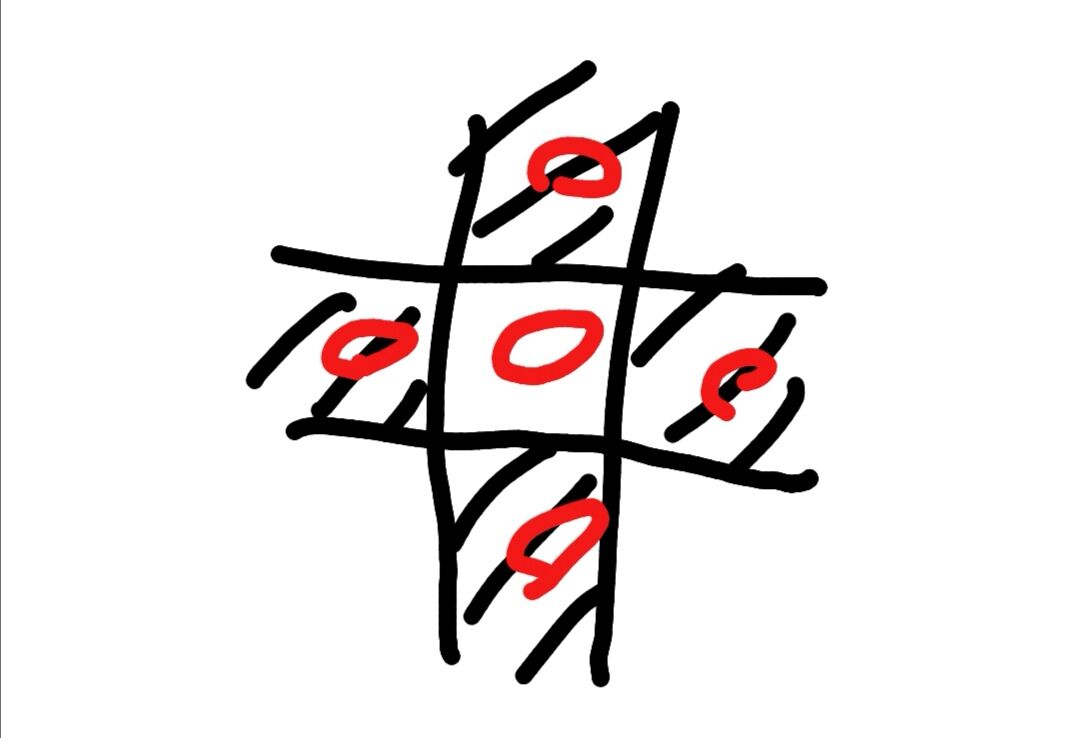

五个同色棋子，白格一个，黑格四个，删白格。
但这种方法还是有badcase。

所以……我也不知道咋做！

  • 参考代码:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #include<iostream>
    #include<algorithm>

    using namespace std;


    int main() {
        
        return 0;
    }
 Previous

Simulation