总结LeetCode上买卖股票这一类型的几道题

2021-11-21

Algorithm

第一题

LeetCode 121 Easy [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock/ ]

描述：

给一个数组，数组中的第i个元素代表第i天的股票价格。如果只允许完全至多一次交易（即买进一股股票并卖出这股股票），那么最大收益是多少？

注意：卖出股票的时间不能早于买进股票的时间。

输入：

一个数组。
输出：

买卖股票的最大收益。
样例输入1：

[7,1,5,3,6,4]
样例输出1：

5
样例输入2：

[7,6,4,3,1]
样例输出2：

0
解题思路：贪心法

遍历一次数组，用一个变量记录遍历过的数中的最小值，然后每次计算当前值和最小值之间的差值作为利润，每次选较大的利润来更新，遍历完成后，当前利润即所求。

参考代码:

代码1，时间复杂度$O(n^2)$

LeetCode上的数据范围是$1 <= prices.length <= 10^5$，$O(n^2)$时间复杂度的算法会超时，故代码1提交时会TLE

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res=0;
        for(int i=0;i<prices.size()-1;i++) {
            for(int j=i+1;j<prices.size();j++) {
                res=max(res,prices[j]-prices[i]);
            }
        }
        return res;
    }
};

代码2，时间复杂度$O(n)$

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res=0, buy=INT_MAX;
        for(auto& price:prices) {
            buy=min(buy,price);
            res=max(res,price-buy);
        }
        return res;
    }
};

第二题

LeetCode 122 Easy [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/ ]

描述：

给一个数组，数组中的第i个元素代表第i天的股票价格。如果允许完成多次交易（即多次买进一股股票并卖出这股股票），那么最大收益是多少？

注意：不能同时进行多次交易，必须在再次买进股票前卖出股票。
输入：

一个数组。
输出：

买卖股票的最大收益。
输入样例1：

[7,1,5,3,6,4]
输出样例1：

7

说明：第二天买进，第三天卖出，获得收益5-1=4；第四天买进，第五天卖出，获得收益6-3=3。总共获得收益4+3=7。
输入样例2：

[1,2,3,4,5]
输出样例2：

4

说明：第一天买进，第五天卖出，获得收益5-1=4。不能在第一天买进，第二天买进，稍后再卖出它们，因为这算同时进行多次交易。
输入样例3：

[7,6,4,3,1]
输出样例3：

0
解题思路：贪心法

从第二天开始，如果当前价格比之前价格高，则把差值加入利润中，因为我们可以昨天买入，今日卖出，若明日价更高的话，还可以今日买入，明日再抛出。以此类推，遍历完整个数组后即可求得最大利润。

参考代码：

代码1，时间复杂度$O(n)$

class Solution {
public:
    int maxProfit(vector<int>& prices){
        int sum=0;
        for(int i=1;i<prices.size();i++) {
            if(prices[i]>prices[i-1])
                sum+=prices[i]-prices[i-1];
        }
        return sum;
    }
};

代码2

class Solution {
public:
    int maxProfit(vector<int>& prices){
        int sum=0;
        for(int i=1;i<prices.size();i++) {
            sum+=max(0,prices[i]-prices[i-1]);
        }
        return sum;
    }
};

代码3，类比第一题

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int sell=0,buy=INT_MIN;
        for(int p:prices) {
            buy=max(buy,sell-p);
            sell=max(sell,buy+p);
        }
        return sell;
    }
};

第三题

LeetCode 123 Hard [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/ ]

描述：

给一个数组，数组中的第i个元素代表第i天的股票价格。如果只允许完成最多两次交易（即最多两次买进股票并卖出股票），那么最大收益是多少？

注意：不能同时进行多次交易，必须在再次买进股票前卖出股票。
输入：

一个数组。
输出：

买卖股票的最大收益。
输入样例1：

[3,3,5,0,0,3,1,4]
输出样例1：

6

说明：第四天买进，第六天卖出，获得收益3-0=3；然后第七天买进，第八天卖出，获得收益4-1=3。总共获得收益3+3=6。
输入样例2：

[1,2,3,4,5]
输出样例2：

4

说明：第一天买进，第五天卖出，获得收益5-1=4。不能在第一天买进，第二天买进，稍后再卖出它们，因为这算同时进行多次交易。
输入样例3：

[7,6,4,3,1]
输出样例3：

0
解题思路：动态规划

题目规定最多交易两次，而不是一定要交易两次，故允许在同一天既买进又卖出，这相当于不交易

因为最多允许两次交易且交易分先后，所以可将区间分成两段，分别使用动态规划求每段的最大利润

f[i]表示在第i天一定卖出时的最大利润，即区间[0, i]的最大利润

g[i]表示在第i天买入且在最后一天一定卖出时的最大利润，即区间[i, n-1]的最大利润

那么，max{f[i]+g[i]}就是最多允许两次交易的最大利润

参考代码：

代码1，时间复杂度O(n)，空间复杂度O(n)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()<2)return 0;
        const int n=prices.size();
        vector<int> f(n,0);
        vector<int> g(n,0);
        for(int i=1,valley=prices[0];i<n;i++) {
            valley=min(valley,prices[i]);
            // 第i天一定卖出的最大利润 包括 第i-1天一定卖出的最大利润
            f[i]=max(f[i-1],prices[i]-valley);
        }
        for(int i=n-2,peak=prices[n-1];i>=0;i--) {
            peak=max(peak,prices[i]);
            // 第i天买入且最后一天一定卖出的最大利润 不包括 第i+1天买入且最后一天卖出的最大利润
            g[i]=max(g[i],peak-prices[i]);
        }
        int max_profit=0;
        for(int i=0;i<n;i++)
            max_profit=max(max_profit,f[i]+g[i]);
        return max_profit;
    }
};

代码2，第四题代码2的特例，将k改成2所得

class Solution {
public:
    int maxProfit(vector<int>& prices) {
    	vector<int> sells(3,0), buys(3,INT_MIN);
		for(int p:prices) {
            for(int i=1;i<=2;i++) {
                buys[i]=max(buys[i],sells[i-1]-p);
            	sells[i]=max(sells[i],buys[i]+p);
        	}
        }
        return sells[2];
    }
};

第四题

LeetCode 188 Hard [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/ ]

描述：

给一个数组，数组中的第i个元素代表第i天的股票价格。如果只允许完成最多k次交易（即最多k次买进股票并卖出股票），那么最大收益是多少？

注意：不能同时进行多次交易，必须在再次买进股票前卖出股票。
输入：

一个数组和一个数，用空格分隔。
输出：

买卖股票的最大收益。
输入样例1：

[2,4,1] 2
输出样例1：

2

说明：第一天买进，第二天卖出，总共获得收益4-2=2。
输入样例2：

[3,2,6,5,0,3] 2
输出样例2：

7

说明：第二天买进，第三天卖出，获得收益6-2=4；然后在第五天买进，第六天卖出，获得收益3-0=3。总共获得收益4+3=7。
解题思路：动态规划

这道题是第三题的推广
如果k的值远大于prices的天数，应该直接用第二题的解法，所以这道题又是第二题和第三题的结合

参考代码：

代码1

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.empty()) return 0;
        const int n=prices.size();
        if(k>=n) return solveMaxProfit(prices);
        int global[k+1]={0};
        int local[k+1]={0};
        for(int i=0;i<n-1;i++) {
            int diff=prices[i+1]-prices[i];
            for(int j=k;j>=1;j--) {
                local[j]=max(global[j-1]+max(diff,0),local[j]+diff);
                global[j]=max(global[j],local[j]);
            }
        }
        return global[k];
    }
    int solveMaxProfit(vector<int>& prices) {
        int res=0;
        for(int i=1;i<prices.size();i++) {
            if(prices[i]-prices[i-1]>0) {
                res+=prices[i]-prices[i-1];
            }
        }
        return res;
    }
};

代码2

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
    	if(k>=prices.size()/2) return helper(prices);
        vector<int> sells(k+1,0),buys(k+1,INT_MIN);
        for(int p:prices) {
        	for(int i=1;i<=k;i++) {
                // buys[i]表示在价格为p时第i次买入的最大利润
                // sells[i]表示在价格为p是第i次卖出的最大利润
                buys[i]=max(buys[i],sells[i-1]-p);
            	sells[i]=max(sells[i],buys[i]+p);
        	}
        }
        return sells[k];
    }
    int helper(vector<int>& prices) {
        int res=0;
        for(int i=1;i<prices.size();i++) {
            res+=max(0,prices[i]-prices[i-1]);
        }
        return res;
    }
};

第五题

LeetCode 309 Medium [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/ ]

描述：

给一个数组，数组中的第i个元素代表第i天的股票价格。如果允许按照以下限制完成多次交易（即多次买进股票并卖出股票），那么最大收益是多少？

限制1：不能同时进行多次交易，必须在再次买进股票前卖出股票。
限制2：在卖出股票后，不能买进下一天的股票（冷却一天）。
输入：

一个数组。
输出：

买卖股票的最大收益。
输入样例：

[1,2,3,0,2]
输出样例：

3

说明：第一天买进，第二天卖出，第三天冷却，第四天买进，第五天卖出，总共获得收益1+2=3。
解题思路：动态规划

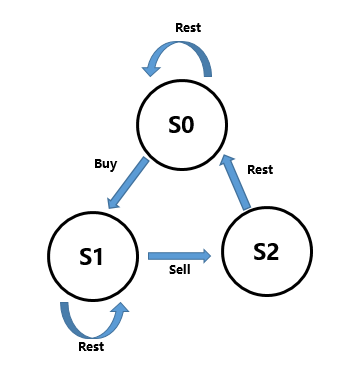
状态转移图中：
S0 代表没有买入的状态
S1 代表买入后等待卖出的状态
S2 代表卖出后的状态

S2与S0的区别是：因为题目要求卖出后必须cooldown一轮，所以卖出进入S2后，必须再进入S0这个等待买入的状态，这一状态转换代表cooldown一轮

状态转移方程：
$s0[i] = max(s0[i-1], s2[i-1])$
$s1[i] = max(s1[i-1], s0[i-1] - price[i])$
$s2[i] = s1[i-1] + price[i]$

参考代码：

代码1

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        const int n=prices.size();
        if(n<=1) return 0;
        vector<int> s0(n,0);
        vector<int> s1(n,0);
        vector<int> s2(n,0);
        s1[0]=-prices[0];
        s0[0]=0;
        s2[0]=INT_MIN;
        for(int i=1;i<n;i++) {
            s0[i]=max(s0[i-1],s2[i-1]);
            s1[i]=max(s1[i-1],s0[i-1]-prices[i]);
            s2[i]=s1[i-1]+prices[i];
        }
        return max(s0[n-1],s2[n-1]);
    }
};

代码2，类比第四题代码2，两个数组意思不同

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len=prices.size();
        vector<int> sell(len+1,0),buy(len+1,INT_MIN);
        for(int i=1;i<len+1;i++) {
            // buy[i]表示第i-1天持股的最大利润
            // sell[i]表示第i-1天未持股的最大利润
            buy[i]=max(buy[i-1],(i-2>0?sell[i-2]:0)-prices[i-1]); //i-2>=0也可以
            sell[i]=max(sell[i-1],buy[i-1]+prices[i-1]);
        }
        return sell[len];
    }
};

第六题

LeetCode 714 Medium [ https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/ ]

描述：

给一个数组和一个数，数组中的第i个元素代表第i天的股票价格，那个数代表交易费。如果允许完成多次交易（即多次买进股票并卖出股票），且每次交易需要支付交易费，那么最大收益是多少？

注意：不能同时进行多次交易，必须在再次买进股票前卖出股票。
输入：

一个数组prices（$0 < prices.length \le 50000$，$0 < prices[i] < 50000$）和一个数fee（$0 \le fee < 50000$），用空格分隔。
输出：

买卖股票的最大收益。
输入样例：

[1,3,2,8,4,9] 2
输出样例：

8

说明：第一天买进，第四天卖出，第五天买进，第六天卖出，总共获得收益(8-1-2)+(9-4-2)=8。
解题思路：动态规划

贪心法不行，当卖出的利润小于交易费时，不应该卖出，否则会亏损。

状态转移方程：
$sold[i] = max(sold[i - 1], hold[i - 1] + prices[i] - fee)$
$hold[i] = max(hold[i - 1], sold[i - 1] - prices[i])$

不管是卖出还是保留，第i天的利润只跟第i-1天有关系，所以可以优化空间，用两个变量来表示当前的卖出和保留的利润，

参考代码：

代码1

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int sold=0,hold=-prices[0];// hold=INT_MIN也可以
        for(int price:prices) {
            int t=sold;
            sold=max(sold,hold+price-fee);
            hold=max(hold,t-price);
        }
        return sold;
    }
};

代码2，类比第二题代码3

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int sold=0,hold=-prices[0];// hold=INT_MIN也可以
        for(int price:prices) {
            hold=max(hold,sold-price);
            sold=max(sold,hold+price-fee);
        }
        return sold;
    }
};

总结LeetCode上买卖股票这一类型的几道题

第一题

第二题

第三题

第四题

第五题

第六题

Previous

总结LeetCode上跳跃游戏这一类型的几道题

DFS Dynamic Programming Greedy BFS LeetCode

Next

YAPI——api自动化测试平台

Golang Microservice

Related Posts