第一题
LeetCode 55 Medium [ https://leetcode.com/problems/jump-game ]
描述:
给定一个非负整数数组
nums,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
输入:
一个非负整数数组
输出:
true 或 false
样例输入1:
[2,3,1,1,4]
样例输出1:
true
说明:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
样例输入2:
[3,2,1,0,4]
样例输出2:
false
说明:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
数据范围
$1 <= nums.length <= 10^4$
$0 <= nums[i] <= 10^5$
解题思路:贪心法
用动态规划也可解此题,但最好的方法还是贪心,只关心能否到达末尾即可。
参考代码:
代码1,时间复杂度$O(n)$
1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
bool canJump(vector<int>& nums) {
int n=nums.size(),reach=0;
for(int i=0;i<n;i++) {
if(i>reach || reach>=n-1) break;
reach=max(reach,i+nums[i]);
}
return reach>=n-1;
}
};
第二题
LeetCode 45 Medium [ https://leetcode.com/problems/jump-game-ii ]
描述:
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
输入:
一个非负整数数组
输出:
一个整数
输入样例1:
[2,3,1,1,4]
输出样例1:
2
说明:跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
输入样例2:
[2,3,0,1,4]
输出样例2:
2
数据范围:
$1 <= nums.length <= 10^4$
$0 <= nums[i] <= 1000$
解题思路:贪心法
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int jump(vector<int>& nums) {
int n=nums.size(),res=0,i=0,cur=0;
while(cur<n-1) {
res++;
int pre=cur;
for(;i<=pre;i++) {
cur=max(cur,i+nums[i]);
}
if(cur==pre) return -1;
}
return res;
}
};
第三题
LeetCode 1306 Hard [ https://leetcode.com/problems/jump-game-iii ]
描述:
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
输入:
一个非负整数数组和一个整数
输出:
true 或 false
输入样例1:
[4,2,3,0,3,1,2] 5
输出样例1:
true
说明:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3输入样例2:
[3,0,2,1,2] 2
输出样例2:
false
说明:无法到达值为 0 的下标 1 处。
数据范围:
$1 <= arr.length <= 5 * 10^4$
$0 <= arr[i] < arr.length$
$0 <= start < arr.length$
解题思路:DFS
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
bool canReach(vector<int>& arr, int start) {
int n=arr.size();
vector<bool> visited(n);
return helper(arr,visited,start);
}
bool helper(vector<int>& arr, vector<bool>& visited, int start) {
if(arr[start]==0) return true;
if(visited[start]) return false;
visited[start]=true;
bool flag=false;
if(start-arr[start]>=0)
flag = flag || helper(arr,visited,start-arr[start]);
if(start+arr[start]<arr.size())
flag = flag || helper(arr,visited,start+arr[start]);
return flag;
}
};
第四题
LeetCode 1345 Hard [ https://leetcode.com/problems/jump-game-iv ]
描述:
给你一个整数数组 arr ,你一开始在数组的第一个元素处(下标为 0)。
每一步,你可以从下标 i 跳到下标:
i + 1 满足:i + 1 < arr.length
i - 1 满足:i - 1 >= 0
j 满足:arr[i] == arr[j] 且 i != j
请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。注意:任何时候你都不能跳到数组外面。
输入:
一个整数数组
输出:
一个整数
输入样例1:
[100,-23,-23,404,100,23,23,23,3,404]
输出样例1:
3
说明:那你需要跳跃 3 次,下标依次为 0 –> 4 –> 3 –> 9 。下标 9 为数组的最后一个元素的下标。
输入样例2:
[7]
输出样例2:
0
说明:一开始就在最后一个元素处,所以你不需要跳跃。
输入样例3:
[7,6,9,6,9,6,9,7]
输出样例3:
1
说明:你可以直接从下标 0 处跳到下标 7 处,也就是数组的最后一个元素处。
输入样例4:
[6,1,9]
输出样例4:
2
输入样例5:
[11,22,7,7,7,7,7,7,7,22,13]
输出样例5:
3
数据范围:
$1 <= arr.length <= 5 * 10^4$
$-10^8 <= arr[i] <= 10^8$
解题思路:BFS
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
int minJumps(vector<int>& arr) {
int res=INT_MAX,n=arr.size(),cur=0;
vector<bool> visited(n);
unordered_map<int,vector<int>> m;
for(int i=0;i<n;i++) {
m[arr[i]].push_back(i);
}
queue<int> q{{0}};
visited[0]=true;
while(!q.empty()) {
for(int i=q.size();i>0;i--) {
int t=q.front();q.pop();
if(t==n-1) {
res=min(res,cur);
}
if(t-1>=0 && !visited[t-1]) {
q.push(t-1);
visited[t-1]=true;
}
if(t+1<n && !visited[t+1]) {
q.push(t+1);
visited[t+1]=true;
}
for(int v:m[arr[t]]) {
if(v!=t && !visited[v]) {
q.push(v);
visited[v]=true;
}
}
m[arr[t]].clear();
}
++cur;
}
return res;
}
};
第五题
LeetCode 1340 Hard [ https://leetcode.com/problems/jump-game-v ]
描述:
给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到:
i + x ,其中 i + x < arr.length 且 0 < x <= d 。
i - x ,其中 i - x >= 0 且 0 < x <= d 。
除此以外,你从下标 i 跳到下标 j 需要满足:arr[i] > arr[j] 且 arr[i] > arr[k] ,其中下标 k 是所有 i 到 j 之间的数字(更正式的,min(i, j) < k < max(i, j))。你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。
请注意,任何时刻你都不能跳到数组的外面。
输入:
一个整数数组和一个整数
输出:
一个整数
输入样例1:
[6,4,14,6,8,13,9,7,10,6,12] 2
输出样例1:
4
说明:
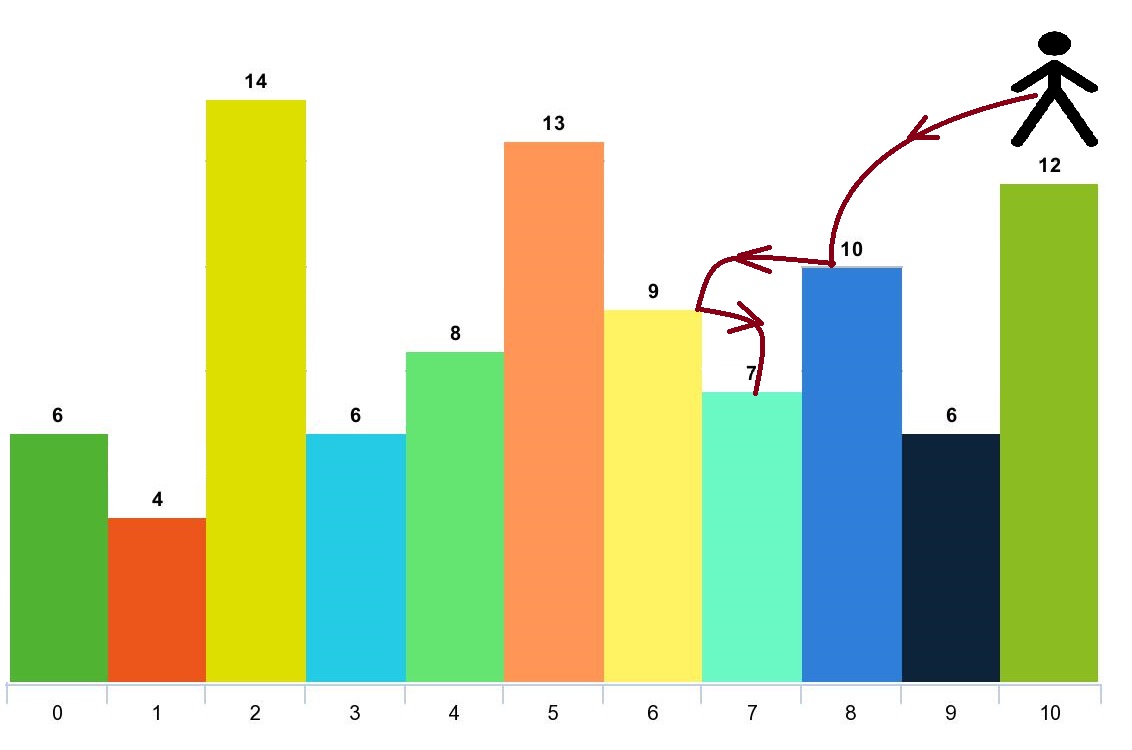
你可以从下标 10 出发,然后如上图依次经过 10 –> 8 –> 6 –> 7 。
注意,如果你从下标 6 开始,你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处,因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的,你不能从下标 3 处跳到下标 2 或者下标 1 处。输入样例2:
[3,3,3,3,3] 3
输出样例2:
1
输入样例3:
[7,6,5,4,3,2,1] 1
输出样例3:
7
输入样例4:
[7,1,7,1,7,1] 2
输出样例4:
2
输入样例5:
[66] 1
输出样例5:
1
数据范围:
$1 <= arr.length <= 1000$
$1 <= arr[i] <= 10^5$
$1 <= d <= arr.length$
解题思路:动态规划
用 $dp[i]$ 表示从 $i$ 开始跳,最多可以跳的台阶数。
因为,根据题意只能往低了跳,且中间不能遇到比自己高的,所以,动态规划要按从低向高的顺序计算,要先排序(这一点很重要),这里借助multimap数据结构进行排序,默认升序排列。
状态转移方程 $dp[i]=max(dp[i], 1+dp[j])$,从 $i$ 跳到所有可能的 $j$参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int maxJumps(vector<int>& arr, int d) {
int n=arr.size();
vector<int> dp(n); // dp数组
multimap<int,int> m;
for(int i=0;i<n;i++) {
m.insert(make_pair(arr[i],i));
}
for(auto& it:m) { // 从低到高开始dp
int i=it.second;
dp[i]=1; // 至少为1,因为至少包含自身
for(int j=i-1;j>=i-d && j>=0 && arr[j]<arr[i];j--) {
// 往左边找比自己低的,遇到比自己高的就停止
// 由于由低到高计算,比自己低的已经计算好了
dp[i]=max(dp[i],1+dp[j]);
}
for(int j=i+1;j<=i+d && j<n && arr[j]<arr[i];j++) {
// 往右边找比自己低的,遇到比自己高的就停止
// 由于由低到高计算,比自己低的已经计算好了
dp[i]=max(dp[i],1+dp[j]);
}
}
return *max_element(dp.begin(),dp.end());
}
};
第六题
LeetCode 1696 Medium [ https://leetcode.com/problems/jump-game-vi ]
描述:
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
一开始你在下标 0 处。每一步,你最多可以往前跳 k 步,但你不能跳出数组的边界。也就是说,你可以从下标 i 跳到 [i + 1, min(n - 1, i + k)] 包含 两个端点的任意位置。
你的目标是到达数组最后一个位置(下标为 n - 1 ),你的 得分 为经过的所有数字之和。
请你返回你能得到的 最大得分 。
输入:
一个整数数组和一个整数
输出:
一个整数
输入样例1:
[1,-1,-2,4,-7,3] 2
输出样例1:
7
说明:你可以选择子序列 [1,-1,4,3] ,和为 7 。
输入样例2:
[10,-5,-2,4,0,3] 3
输出样例2:
17
输入样例3:
[1,-5,-20,4,-1,3,-6,-3] 2
输出样例3:
0
数据范围:
$1 <= nums.length, k <= 10^5$
$-10^4 <= nums[i] <= 10^4$
解题思路:动态规划
这题很容易想到 DP,但是 DP 的复杂度是 $O(n*k)$ 的,显然会超时,所以要借助一种数据结构快速找到[i−k, i−1]的最大值,然后再结合 DP 即可。
这种数据结构可以是堆,也可以是单调队列。用堆的话,堆顶维护区间最大值,把下标也一并放入堆中来帮助判断是否能从这个状态转移;用单调队列的话,队首维护区间最大值,按需出队、入队皆可。
参考代码:
代码1,时间复杂度$O(n*k)$
LeetCode上的数据范围是$1 <= nums.length, k <= 10^5$,$O(n*k)$时间复杂度的算法会超时,故代码1提交时会TLE
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxResult(vector<int>& nums, int k) {
int n=nums.size();
vector<int> dp(n,INT_MIN);
dp[n-1]=nums[n-1];
for(int i=n-1;i>=0;i--) {
for(int j=1;j<=k && i+j<n;j++) {
dp[i]=max(dp[i],nums[i]+dp[i+j]);
}
}
return dp[0];
}
};代码2,时间复杂度$O(nlogn)$,动态规划+堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int maxResult(vector<int>& nums, int k) {
int n=nums.size();
vector<int> dp(n,0);
dp[0]=nums[0];
priority_queue<pair<int,int>> pq;
pq.push({nums[0],0});
for(int i=1;i<n;i++) {
while(pq.top().second<i-k) pq.pop();
dp[i]=nums[i]+pq.top().first;
pq.push({dp[i],i});
}
return dp[n-1];
}
};代码3,每个元素只会入队列一次和出队列一次,所以总体时间复杂度$O(n)$,动态规划+滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxResult(vector<int>& nums, int k) {
int n=nums.size();
vector<int> dp(n,0);
dp[0]=nums[0];
deque<int> dq;
dq.push_back(0);
for(int i=1;i<n;i++) {
while(i-k>dq.front()) dq.pop_front();
dp[i]=nums[i]+dp[dq.front()];
while(dq.size() && dp[i]>dp[dq.back()]) dq.pop_back();
dq.push_back(i);
}
return dp[n-1];
}
};
第七题
LeetCode 1871 Medium [ https://leetcode.com/problems/jump-game-vii ]
描述:
给你一个下标从 0 开始的二进制字符串 s 和两个整数 minJump 和 maxJump 。一开始,你在下标 0 处,且该位置的值一定为 ‘0’ 。当同时满足如下条件时,你可以从下标 i 移动到下标 j 处:
- i + minJump <= j <= min(i + maxJump, s.length - 1) 且
- s[j] == ‘0’.
如果你可以到达 s 的下标 s.length - 1 处,请你返回 true ,否则返回 false 。
输入:
一个字符串和两个整数
输出:
true 或 false
输入样例1:
“011010” 2 3
输出样例1:
true
说明:第一步,从下标 0 移动到下标 3 。第二步,从下标 3 移动到下标 5 。
输入样例2:
“01101110” 2 3
输出样例2:
false
数据范围:
$2 <= s.length <= 10^5$
s[i] 要么是 ‘0’ ,要么是 ‘1’
s[0] == ‘0’
$1 <= minJump <= maxJump < s.length$解题思路:贪心+剪枝优化
首先要明白,末尾字符为’1’的话一定返回false。因为只能跳到字符为’0’的位置,如果末尾字符为’1’,则表示永远跳不到末尾。
然后遍历字符串,标记在每个位置上能跳跃到的位置。可以使用额外的数组来标记,也可以直接在原字符串进行标记。
一开始这样是会超时的,有很多位置可能存在重复标记。因此做一个小小的优化,在标记前比较本次标记的起始位置与已标记到的位置,取较大值作为新的标记起始位置,这样可以避免重复标记之前已标记过的位置。
最后看末尾位置是否已标记,如果已标记,说明能够到达末尾。
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
bool canReach(string s, int minJump, int maxJump) {
int n=s.size(), j=0;
if(s[n-1]=='1') return false;
vector<bool> visited(n);
visited[0]=true;//初始必须标记位置0,否则循环中的判断会导致出错
for(int i=0;i<n;i++) {
if(s[i]=='1') continue; //该位置的字符为'1',则无法跳到此位置
if(!visited[i]) continue; //此位置未标记,表示从起始位置无法跳到此位置
for(j=max(j,i+minJump);j<=min(i+maxJump,n-1);j++) {
if(s[j]=='0') visited[j]=true;
}
if(visited[n-1]) return true;
}
return visited[n-1];
}
};